(Java) 백준 2263 트리의 순회

트리의 순회

이진 트리의 인오더와 포스트오더가 주어졌을 때, 프리오더를 구하는 문제이다.

인오더는 중위 순회를, 포스트오더는 후위 순회를, 프리오더는 전위 순회를 의미한다.

중위 순회는 left -> root -> right 순으로 순회,

후위 순회는 left -> right -> root 순으로 순회,

전위 순회는 root -> left -> right 순으로 순회하는 것이다.

 

이 문제는 중위 순회와 후위 순회의 특징을 이용해 트리의 구조를 파악하여 푸는 문제이다.
중위 순회와 후위 순회의 공통 부분은 left부터 순회를 시작하는 것.

즉, 순회 시작부분은 둘이 같다.
후위 순회의 경우 가장 마지막 순회 노드가 루트 노드이고,

중위 순회는 루트노드가 왼쪽 트리와 오른쪽 트리를 나누는 중간 노드이므로,

후위 순회를 통해 루트 노드를 찾고, 중위 순회에서 왼쪽 트리 오른쪽 트리로 분할하여 트리 구조를 파악할 수 있다.

 

한눈에 알아보기 쉬운 자료가 있어 가져와봤다.

출처 : https://velog.io/@dark6ro/%EB%B0%B1%EC%A4%80-2263%EB%B2%88-%ED%8A%B8%EB%A6%AC%EC%9D%98-%EC%88%9C%ED%9A%8C

 

 

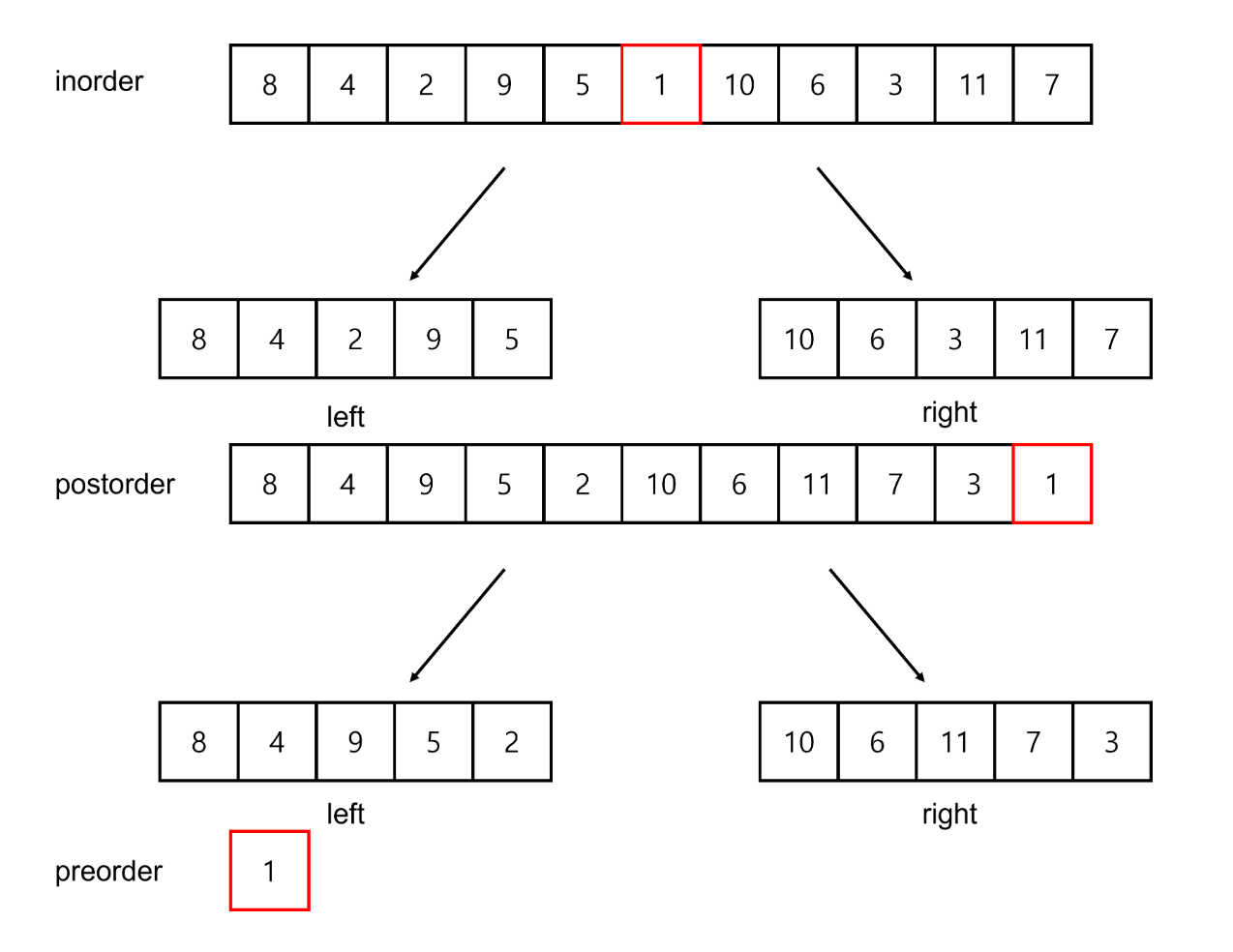
import java.io.*;
import java.util.*;

public class Main {

    static int N, preOrderIdx;
    static int[] inOrder, postOrder, preOrder;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        StringBuilder sb = new StringBuilder();

        N = Integer.parseInt(br.readLine());
        inOrder = new int[N+1];   // 중위 순회 : left -> root -> right
        postOrder = new int[N+1]; // 후위 순회 : left -> right -> root
        preOrder = new int[N+1];  // 전위 순회 : root -> left -> right

        st = new StringTokenizer(br.readLine());
        for(int i = 1; i <= N; i++) {
            inOrder[i] = Integer.parseInt(st.nextToken());
        }

        st = new StringTokenizer(br.readLine());
        for(int i = 1; i <= N; i++) {
            postOrder[i] = Integer.parseInt(st.nextToken());
        }

        preOrderIdx = 1;
        searchPreOrder(1, N, 1, N);

        for(int i = 1; i <= N; i++) {
            sb.append(preOrder[i] + " ");
        }
        System.out.println(sb);
    }

    static void searchPreOrder(int inOrderStart, int inOrderEnd, int postOrderStart, int postOrderEnd) {
        if(inOrderStart <= inOrderEnd && postOrderStart <= postOrderEnd) {
            preOrder[preOrderIdx++] = postOrder[postOrderEnd];

            int inOrderParentIdx = inOrderStart;
            for(int i = inOrderStart; i <= inOrderEnd; i++) {
                if(postOrder[postOrderEnd] == inOrder[i]) {
                    inOrderParentIdx = i;
                    break;
                }
            }

            // left
            searchPreOrder(inOrderStart, inOrderParentIdx-1, postOrderStart, postOrderStart + inOrderParentIdx - inOrderStart - 1);
            // right
            searchPreOrder(inOrderParentIdx+1, inOrderEnd, postOrderEnd-inOrderEnd+inOrderParentIdx, postOrderEnd-1);
        }
    }
}

 

디버깅

1. 처음엔 중위 순회 배열과 후위 순회 배열의 인덱스가 분할하다보면 동일하지 않다는 것을 몰라 해맸다. 이를 해결하고자 분할해나가는 메소드의 파라미터에 중위 순회, 후위 순회의 인덱스로 놨다.

 2. 구하려는 전위 순회 배열의 인덱스를 벗어나는 버그가 발생했다. 탈출조건을 start인덱스 == end인덱스로 해놨더니 벗어나는 경우도 있었다. start인덱스 <= end인덱스 일때만 메소드가 실행되도록 조건을 잡았다.

 

3. 루트 노드를 찾았을 때 중위 순회에서 트리를 좌,우로 분할하는 과정에서 mid + 1 인덱스를 찾게 해놨더니 오른쪽 트리가 없는 경우 배열범위를 벗어나는 오류가 있었다. 배열에 인덱스를 직접 삽입하기보다는 파라미터로 전달해서 메소드 실행 조건에서 걸리도록 만들어서 해결했다.